|
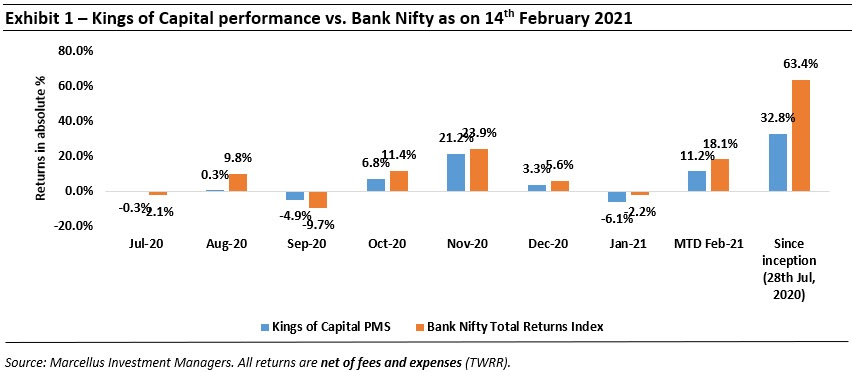 |
|
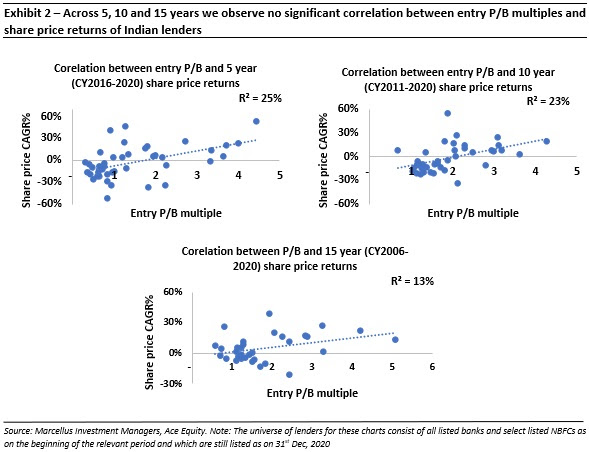
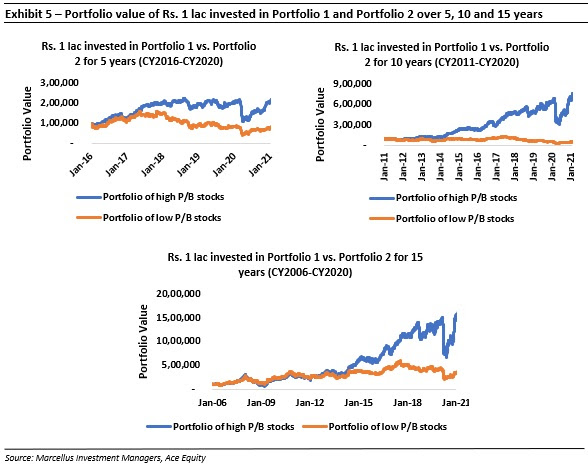
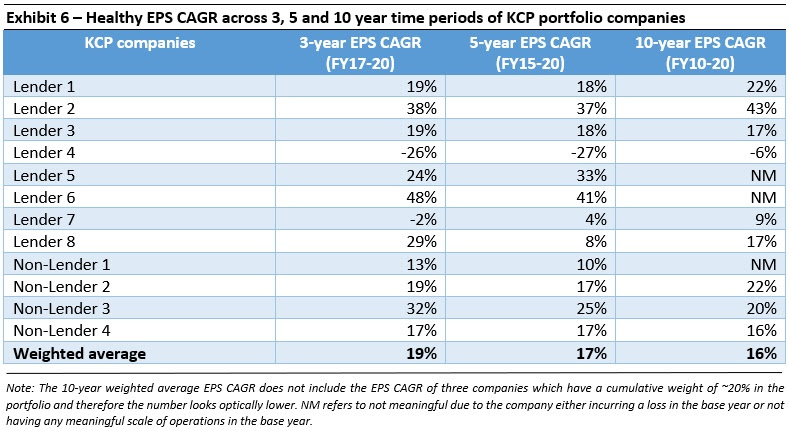
If not entry P/B multiples, then what drives share price returns of Indian lenders?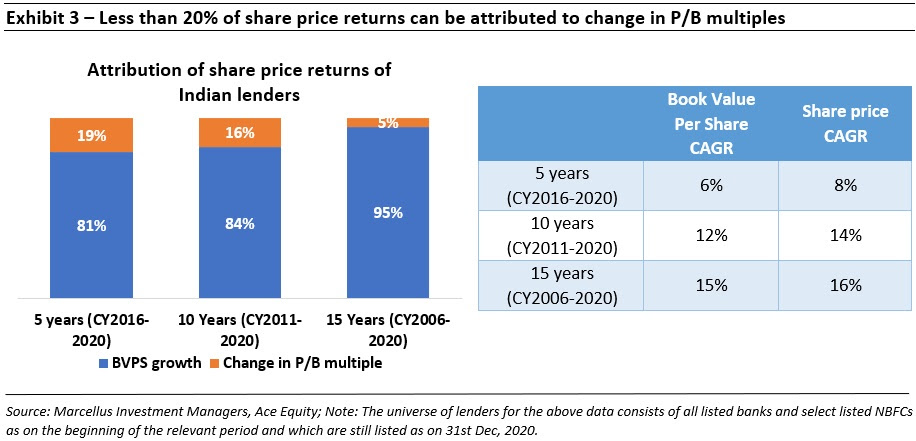 |
|
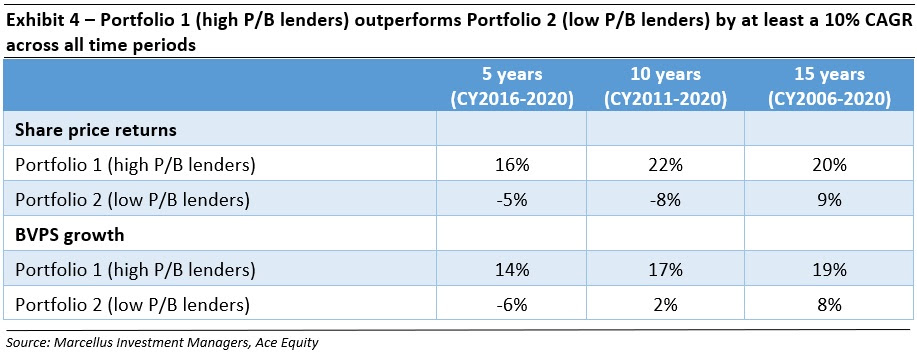 |
Investment implications
Team Marcellus
|
 |
|

If not entry P/B multiples, then what drives share price returns of Indian lenders? |
|
 |


Copyright © 2025 Marcellus Investment Managers Pvt Ltd, All rights reserved
Note: the above material is neither investment research, nor investment advice. Marcellus does not seek payment for or business from this material/email in any shape or form. Marcellus Investment Managers Private Limited (“Marcellus”) is regulated by the Securities and Exchange Board of India (“SEBI”) as a provider of Portfolio Management Services. Marcellus is also a US Securities & Exchange Commission (“US SEC”) registered Investment Advisor. No content of this publication including the performance related information is verified by SEBI or US SEC. If any recipient or reader of this material is based outside India and USA, please note that Marcellus may not be regulated in such jurisdiction and this material is not a solicitation to use Marcellus’s services. This communication is confidential and privileged and is directed to and for the use of the addressee only. The recipient, if not the addressee, should not use this material if erroneously received, and access and use of this material in any manner by anyone other than the addressee is unauthorized. If you are not the intended recipient, please notify the sender by return email and immediately destroy all copies of this message and any attachments and delete it from your computer system, permanently. No liability whatsoever is assumed by Marcellus as a result of the recipient or any other person relying upon the opinion unless otherwise agreed in writing. The recipient acknowledges that Marcellus may be unable to exercise control or ensure or guarantee the integrity of the text of the material/email message and the text is not warranted as to its completeness and accuracy. The material, names and branding of the investment style do not provide any impression or a claim that these products/strategies achieve the respective objectives. Further, past performance is not indicative of future results. Marcellus and/or its associates, the authors of this material (including their relatives) may have financial interest by way of investments in the companies covered in this material. Marcellus does not receive compensation from the companies for their coverage in this material. Marcellus does not provide any market making service to any company covered in this material. In the past 12 months, Marcellus and its associates have never i) managed or co-managed any public offering of securities; ii) have not offered investment banking or merchant banking or brokerage services; or iii) have received any compensation or other benefits from the company or third party in connection with this coverage. Authors of this material have never served the companies in a capacity of a director, officer or an employee.
This material may contain confidential or proprietary information and user shall take prior written consent from Marcellus before any reproduction in any form.
Regards, Team Marcellus
If you want to read our other published material, please visit https://marcellus.in/pms-investment-blog/
Copyright © 2025 Marcellus Investment Managers Pvt Ltd, All rights reserved
RELATED NEWSLETTERS
Earnings Growth in India: Sliding Nifty vs Rising CCP
READ MORE READ MOREPortfolio performance and update on Fundamentals – May 2025
READ MORE READ MOREMeritorQ: Quality Matters
READ MORE READ MORE
 PREV ISSUE
PREV ISSUE